Part 4: The Ugly
Welcome to “the ugly” ACT and SAT problems, the final post in our series comparing ACT and SAT problems at different levels of difficulty. We are going to look at 4 problems, two from each test, some of which are really hard. They might take more work, more reading, integration of more content, or exposure to material that is only covered by math courses that complete an entire year’s curriculum.
Difficult multiple choice problems on both the ACT and SAT will also provide answer options that result from common mistakes that you could make during the problem. We call those “Fool’s Gold” because they look great, but they are actually worthless, point-stealing distractions.
Notice that both problems below are high numbers. The ACT problem is 52/60 while the SAT is 26/30 on the calculator section. These problem numbers can act as a warning for students about the presence of trick questions, fool’s gold answers, and the time that they should spend given a certain target score.

When I, a trained tutor and graduate of engineering school, looked at the ACT Math Hard #1, I didn’t immediately see the solution. So, I used a strategy that we teach every day. I did something that I knew I could do. I wrote down the area of a triangle formula A=12bh and the slope formula m=y2-y1x2-x1. It was a place to start, something that I knew I could do. The ACT Math does require some memorization, and those two equations are absolutely on the list of those you should memorize.
After that, I looked back at the problem. The testers don’t want the area to change when C moves. I visualized C moving across left and right, up and down. My estimation suggested that none of these motions left the area unchanged. Then I looked again at the area equation and remembered that the requirement for the definitions of “base” and “height” require that these two lengths be perpendicular (or meet at a 90 degree angle). Then I imagined each side as the base. I realized that if segment BA was the base, then if the height was to remain unchanged, the point C had to move in a line parallel to segment BA.
Lines that are parallel have the same slope. So, I used the slope formula to calculate the slope of segment BA: m=6-20-8=4-8=-12. Hard problems on ACT can incorporate several concepts or require significant calculations. In the case of this problem, the calculation was simple, the visualization was hard. In my tutoring I sometimes talk about this as the “assessment” or “diagnosis” step in the problem. You guessed it: we have specific techniques to help students improve their ability to assess a problem and choose the correct first step!
ACT Math Hard Answer #2: F, -1/2
Our next problem, SAT Hard #1, incorporates several geometric concepts in three dimensions and requires calculations from an annoyingly complex given. There are a couple places to start on this problem, but I’d recommend starting with the annoyingly complex constant. 6(a4)2 actually holds several hints.
-
A cube has 6 congruent sides (generally sides with equal area), so the area of each individual side is that constant divided by 6 to get (a4)2.
-
Since we are looking for the perimeter, we need to find the side length of one individual side. Since we have the area of one square side, we can use the area of a square equation to find the area of one side length: a=s2.
-
Performing these calculations step by step on paper is a pretty slow and laborious process. However, the constant is set so that a really quick mind can find recognize that if s2=(a4)2 then s=a4.
-
Once we have a single side length, we find the perimeter by multiplying the side length by the number of sides to eventually reduce from the complex start to a basic conclusion: 4s=a4*4=a.
SAT Hard Answer #1 : B - a (answer option B is the variable a)
This type of problem is really typical of the challenging problems. They take a long time if you try to solve the problem systematically, but they can go very quickly if you quickly see to the heart of the problem. A really thorough understanding of the fundamentals of a cube is necessary to even get started on this problem. It takes at least 3 calculations derived from the geometric relationships of a cube and square. The math is super simple-- only if you do every step right and in the right order. Otherwise, you can get bogged down in the calculations.
These “hard” level difficulty problems may have more steps, integrate more concepts, or rely on more advanced material. Regardless, for students looking to score in the high 20s or 30s, mastery of this level of problem is a necessity.
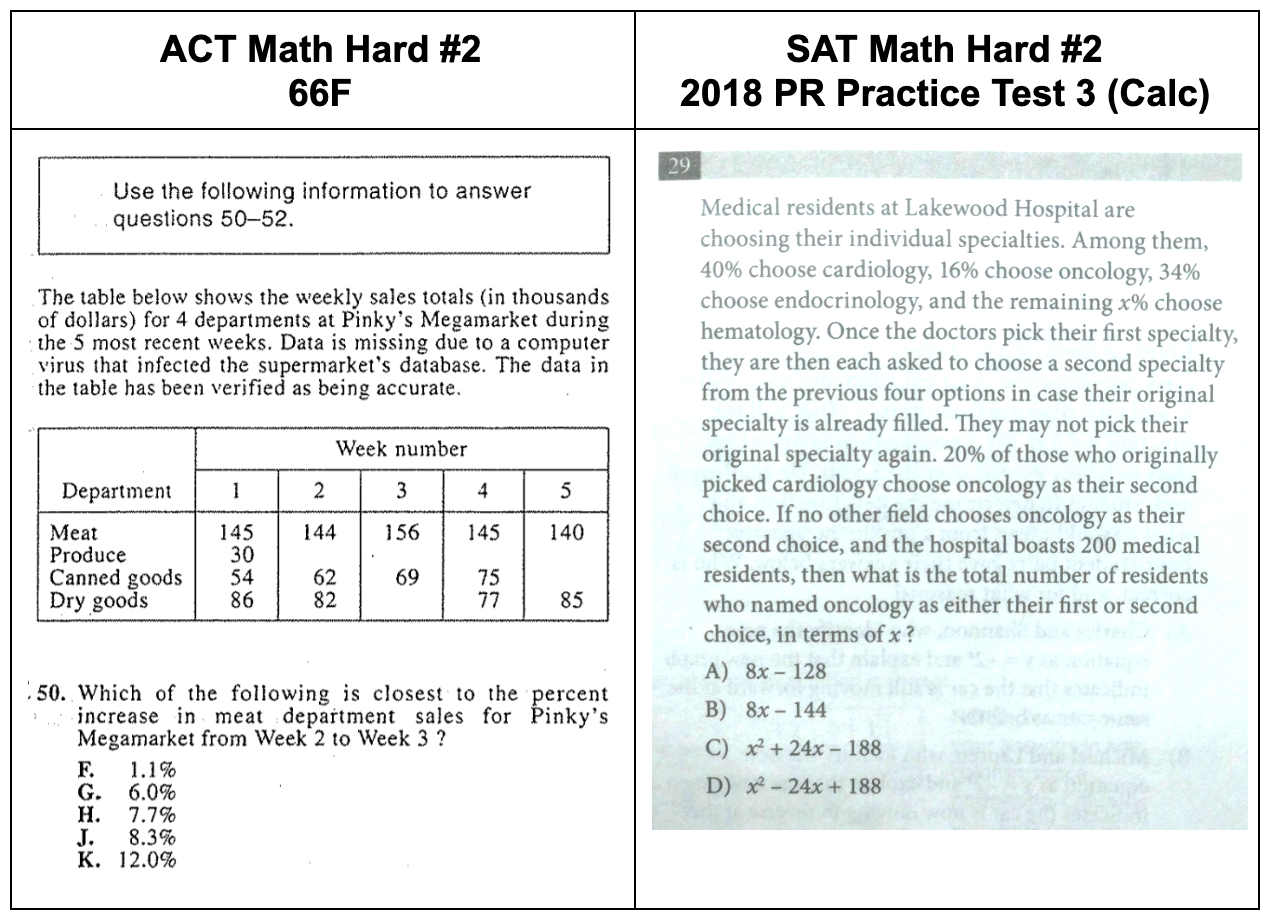
ACT Hard Problem #2 presents one of the ways that the ACT addresses data sets. It is also growing increasingly common for the ACT to provide a large chunk of info, with a table, diagram, or paragraph and then ask several questions about different facets of the info, as they do here (note the problem indicates that 50-52 all use the information).
This specific question asks about percent increase. This is a topic we always discuss during test prep, as it appears with great regularity on the ACT. Sometimes, students will conflate or confuse it with simple percentages; however, percent increases creates a percentage based on how much a given quantity changes as a percent of an original value. The most commonly used reference equation for percent increase uses the following equation: % change=new-originaloriginal*100. Another equation sometimes used to calculate percent change: new=original(1% change100). Both equations convey the same information, just in different forms.
As always, the most important step is to correctly identify the actual information requested by the problem: percent increase in the meat department sales, specifically from week 2 to week 3.
-
In week 2, the meat sales were 144; in week 3 the sales were 156.
-
Use the equation: % change=new-originaloriginal*100.
-
% change=156-144144*100=8.33
If you choose (a) know the correct equation and (b) use it correctly, this problem can be solved quickly and easily. If you don’t, this might be a problem on which you might be forced to guess.
ACT Hard Answer #2: J - 8.3%
The final problem in our review of these is SAT Hard Problem #2. It is 29/30, meaning that it approaches the highest level of difficulty offered in the SAT.
The first challenge in this problem is getting through the veritable wall of text. One helpful strategy is to write down the numbers provided in the material with variables defined so you don’t have to read the text again. Extracting math language from text is a skill in and of itself. You guessed it! That is another skill we train during tutoring.
You should write down something like this: “40% - C , %16 - O, 34% - E, x% - H.” You could also quickly recognize that if x is “the remaining percent” that means that I can find the value of x by adding the other two percentages together and subtracting from 100, because 100 percent represents the total percentage. So, x=100-(40+16+34)=10.
We’ve not yet even gotten to the actual question, so we keep reading! A quick glance at the answer choices reveals that you need to leave your calculations in terms of x. What can you learn from this? Read all the way to the end and find the actual question before you do any calculations.
We get some more information at the bottom of the paragraph. There are 200 students-- simply circling or underlining this number in the text is probably enough emphasis, especially as we are nearing the end of the question. Of the people who chose cardiology, 20% choose oncology as their second choice and no one else chooses oncology.
Finally we get to the actual question: how many students choose oncology as either their first or second choice, in terms of x? Many students will dive right into these calculations.
It is fairly simple to find the number of students who chose oncology in as their first choice using the definition of probability: P(event)=number of specific events total number of events. In this case we know that there are 200 total students and that the probability of one choosing oncology first is 16 percent. You can create the equation: .16=o/200 and solve for “o” by multiplying both sides by 200. This gets us the number of students who choose oncology first: 32.
We can do the same with those who choose oncology second. This time, however, we are choosing from a smaller number of total students, as the problem specifies that “20 percent of those who originally chose cardiology pick oncology [...] second”. That tells us that for those who choose oncology second, the total number of events is the number of people who chose cardiology first: 0.4*200 (40 percent of 200) or 80 people of our original total. 20 percent of those who chose cardiology first is 0.2*(80) or 16 people.
We now know that there were a total of 32+16 =48 people who chose oncology overall. Unfortunately, that doesn’t help us all that much, as all of the answer options have x in them somewhere. Now we can recognize that x=10 and “plug in” to all of those answer options to find which yields a result of 48 if x=10. This process can be slow, but it will eventually get you the right answer.
Of course, there are faster ways to solve this problem more directly. If we use x in the probability calculations we did in the last three paragraphs, we will get an answer in terms of x. A little extra math will tell us which of the provided choices is correct. Unfortunately, I can’t give away all our secrets. If you want to learn other ways to solve this problem, you’ll have to come in to tutoring.
SAT Hard Answer #2: ??? Give it a shot and post your answer in the comments.
Thanks for reading! I hope these posts taught you a little about the SAT and ACT and give you a better idea about how you can prepare for your test. Remember whatever else you do to prepare for these standardized tests, get a good night’s sleep before your test, eat a healthy breakfast the morning you take the test, and bring snacks!
